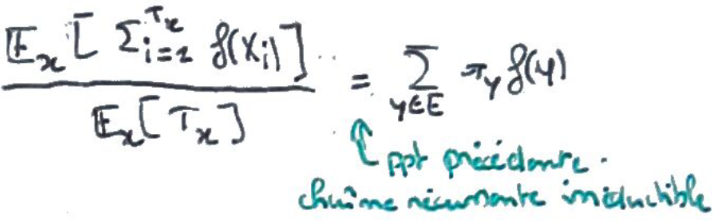On suppose que la fonction est positive.

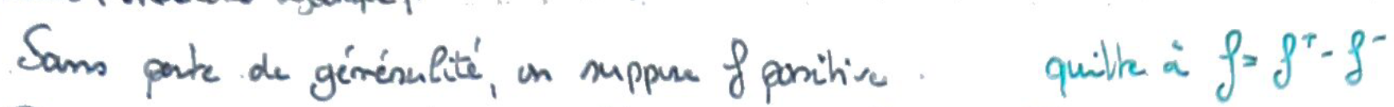
On introduit des notations concernant chaque passage de la chaîne en \(x\).

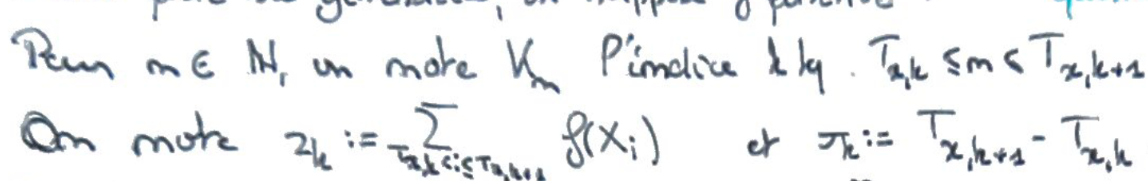
On majore et on minore en enlevant un terme au numérateur ou au dénominateur.

Puisque la chaîne est récurrente irréductible, on a \(K_n\to+\infty\).

En faisant un théorème belge au numérateur et au dénominateur, on peut séparer le minorant et le majorant en termes qui tendent ps vers qqch d'intéressant.

C'est bien la mesure invariante puisque la chaîne est récurrente irréductible \(\to\) ok par théorème des gendarmes.